Planes Geometric Figures Triangles And Quadrilaterals

What are "figuras geometricas planas triangulos y cuadrilateros figuras geometricas planas triangulos y cuadrilateros:"?

In geometry, "figuras geometricas planas triangulos y cuadrilateros figuras geometricas planas triangulos y cuadrilateros:" refers to plane geometric figures that have three or four straight sides, respectively. Triangles have three sides and three angles, while quadrilaterals have four sides and four angles. Both triangles and quadrilaterals are considered two-dimensional shapes with flat surfaces.

Triangles and quadrilaterals are fundamental geometric shapes with various applications in mathematics, engineering, and everyday life. Understanding their properties and relationships is essential for developing spatial reasoning and problem-solving skills.

In this article, we will explore the different types of triangles and quadrilaterals, their properties, and their applications in various fields.

figuras geometricas planas triangulos y cuadrilateros figuras geometricas planas triangulos y cuadrilateros

Plane geometric figures with three or four straight sides are essential in mathematics and various fields. Understanding their properties and relationships is crucial for developing spatial reasoning and problem-solving skills.

• Types: Triangles and quadrilaterals come in various types, each with distinct properties.
• Properties: Triangles have three sides and three angles, while quadrilaterals have four sides and four angles. Both have specific properties related to their side lengths, angles, and diagonals.
• Relationships: Triangles and quadrilaterals can be related hierarchically, with some quadrilaterals (e.g., rectangles) beingof triangles.
• Applications: Triangles and quadrilaterals are widely used in architecture, engineering, design, and everyday life.
• Historical Context: The study of triangles and quadrilaterals dates back to ancient times, with significant contributions from mathematicians like Euclid and Pythagoras.

In conclusion, understanding the key aspects of "figuras geometricas planas triangulos y cuadrilateros figuras geometricas planas triangulos y cuadrilateros:" is essential for developing a strong foundation in geometry. These figures play a vital role in various fields and have a rich historical context. By exploring their types, properties, relationships, applications, and historical significance, we gain a deeper appreciation for their importance in the world around us.

Types

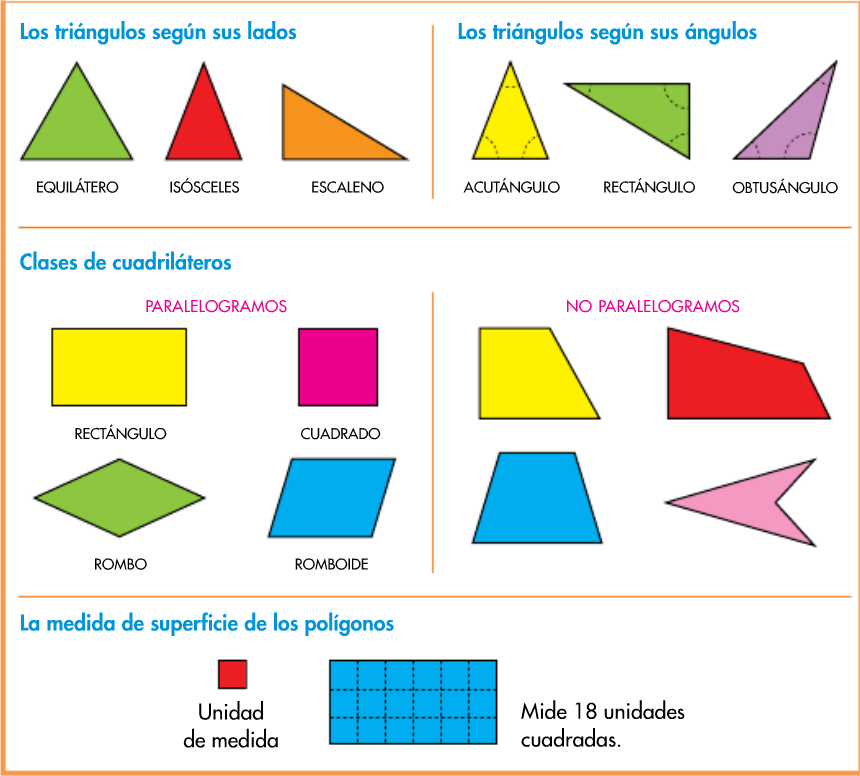
The diversity of triangles and quadrilaterals is a fundamental aspect of "figuras geometricas planas triangulos y cuadrilateros figuras geometricas planas triangulos y cuadrilateros:". Different types of triangles (e.g., equilateral, isosceles, scalene) and quadrilaterals (e.g., squares, rectangles, trapezoids, parallelograms) have unique properties that distinguish them from one another.

Understanding the distinct properties of each type is crucial for solving geometry problems and applying geometric concepts in real-world scenarios. For instance, the properties of equilateral triangles (equal side lengths and angles) are essential in structural engineering to ensure stability and load distribution. Similarly, the properties of rectangles (congruent opposite sides and right angles) are fundamental in architecture and design to create balanced and visually appealing structures.

In conclusion, the exploration of the various types of triangles and quadrilaterals, each with its distinct properties, is a cornerstone of "figuras geometricas planas triangulos y cuadrilateros figuras geometricas planas triangulos y cuadrilateros:". This understanding empowers individuals to analyze and solve geometric problems effectively and apply geometric principles in practical applications across diverse fields.

Properties

The properties of triangles and quadrilaterals, including their side lengths, angles, and diagonals, are fundamental aspects of "figuras geometricas planas triangulos y cuadrilateros figuras geometricas planas triangulos y cuadrilateros:". These properties are essential for understanding the behavior and applications of these geometric shapes across various fields.

For instance, in architecture, the properties of triangles and quadrilaterals are crucial for ensuring structural stability and efficient load distribution. Architects utilize the inherent strength of triangles to design stable structures, such as bridges and buildings. Similarly, the properties of quadrilaterals, such as rectangles and squares, are essential in creating balanced and visually appealing architectural designs.

Furthermore, in engineering, the properties of triangles and quadrilaterals play a vital role in designing and analyzing mechanical systems and components. Engineers rely on the specific properties of these shapes to determine forces, moments, and stresses within structures. Understanding the properties of triangles and quadrilaterals enables engineers to design efficient and reliable systems.

In conclusion, the exploration of the properties of triangles and quadrilaterals is a cornerstone of "figuras geometricas planas triangulos y cuadrilateros figuras geometricas planas triangulos y cuadrilateros:". These properties are not only essential for theoretical understanding but also have significant practical applications in diverse fields, including architecture, engineering, and design.

Relationships

The hierarchical relationship between triangles and quadrilaterals is a fundamental aspect of "figuras geometricas planas triangulos y cuadrilateros figuras geometricas planas triangulos y cuadrilateros:". It provides a deeper understanding of the properties and characteristics of these geometric shapes and their interconnectedness.

• Types of Relationships: Triangles and quadrilaterals can be related in various ways, such as inclusion, inheritance, and specialization. For instance, all rectangles are quadrilaterals, but not all quadrilaterals are rectangles.
• Properties Inheritance: When a quadrilateral is also a triangle (e.g., a rectangle), it inherits the properties of both triangles and quadrilaterals. This allows for a more comprehensive analysis of the shape's behavior and applications.
• Geometric Hierarchy: The hierarchical relationship provides a structured framework for classifying and understanding geometric shapes. It enables mathematicians and researchers to organize and explore the properties of triangles and quadrilaterals systematically.
• Applications in Geometry: The relationships between triangles and quadrilaterals have practical applications in geometry. For example, understanding the hierarchical relationship between rectangles and triangles is essential for solving geometric problems involving area and perimeter calculations.

In conclusion, the exploration of the relationships between triangles and quadrilaterals is a valuable aspect of "figuras geometricas planas triangulos y cuadrilateros figuras geometricas planas triangulos y cuadrilateros:". It provides insights into the properties, inheritance, and applications of these geometric shapes. Understanding these relationships empowers individuals to solve geometric problems effectively and apply geometric principles in diverse fields.

Applications

The practical applications of triangles and quadrilaterals are a fundamental aspect of "figuras geometricas planas triangulos y cuadrilateros figuras geometricas planas triangulos y cuadrilateros:". Understanding these applications is essential for appreciating the relevance and impact of geometry in the real world.

In architecture, the properties of triangles and quadrilaterals are crucial for ensuring structural stability and efficient load distribution. For instance, the triangular shape of trusses and bridges provides strength and rigidity, while the rectangular shape of buildings and rooms creates visually appealing and functional spaces.

In engineering, triangles and quadrilaterals are used in the design and analysis of mechanical systems and components. The triangular shape of gears and the rectangular shape of beams are examples of how these geometric shapes contribute to the functionality and efficiency of engineered systems.

In design, triangles and quadrilaterals are used to create visually appealing and balanced compositions. For instance, the triangular shape of the pyramids in Egypt demonstrates the use of geometry in iconic architectural designs, while the rectangular shape of paintings and photographs is commonly used to create a sense of order and harmony.

In everyday life, triangles and quadrilaterals are found in countless objects and situations. The triangular shape of pizza slices and the rectangular shape of books are just a few examples of how these geometric shapes are integrated into our daily lives.

In conclusion, the exploration of the applications of triangles and quadrilaterals is a valuable aspect of "figuras geometricas planas triangulos y cuadrilateros figuras geometricas planas triangulos y cuadrilateros:". Understanding these applications provides insights into the practical significance of geometry and its impact on various fields and everyday life.

Historical Context

The historical context of triangles and quadrilaterals is deeply intertwined with the development of "figuras geometricas planas triangulos y cuadrilateros figuras geometricas planas triangulos y cuadrilateros:", providing a foundation for understanding their properties and applications.

• Ancient Origins: The study of triangles and quadrilaterals can be traced back to ancient civilizations, such as the Egyptians and Babylonians, who used these shapes in practical applications such as architecture and surveying.

  Euclid's Contributions: The Greek mathematician Euclid played a pivotal role in the development of geometry, including the study of triangles and quadrilaterals. His work, "Elements," provided a systematic framework for understanding geometric shapes and their properties.

  Pythagoras' Theorem: Pythagoras, another renowned Greek mathematician, is famous for his theorem, which relates the lengths of the sides of a right triangle. This theorem has had a profound impact on geometry and its applications in various fields.

  Historical Applications: Throughout history, triangles and quadrilaterals have been used in the design and construction of iconic structures, such as the pyramids of Egypt and the Parthenon in Greece. These shapes provide structural stability and aesthetic appeal, demonstrating the practical significance of geometry in ancient times.

In conclusion, the historical context of triangles and quadrilaterals enriches our understanding of "figuras geometricas planas triangulos y cuadrilateros figuras geometricas planas triangulos y cuadrilateros:". The contributions of ancient mathematicians, such as Euclid and Pythagoras, laid the groundwork for the development of geometry and its applications. By exploring this historical context, we gain a deeper appreciation for the evolution of geometric knowledge and its enduring impact on various fields throughout history.

Frequently Asked Questions about "figuras geometricas planas triangulos y cuadrilateros figuras geometricas planas triangulos y cuadrilateros

This section addresses common questions and misconceptions related to "figuras geometricas planas triangulos y cuadrilateros figuras geometricas planas triangulos y cuadrilateros:".

Question 1: What is the difference between a triangle and a quadrilateral?

Answer: A triangle has three sides and three angles, while a quadrilateral has four sides and four angles. Triangles are classified based on their side lengths (equilateral, isosceles, scalene) and angles (acute, right, obtuse), while quadrilaterals are classified based on their side lengths and angles (squares, rectangles, parallelograms, trapezoids).

Question 2: What are the properties of a rectangle?

Answer: A rectangle is a quadrilateral with four right angles and opposite sides of equal length. Rectangles have two pairs of parallel sides and two pairs of congruent sides. The diagonals of a rectangle are equal in length and bisect each other.

Question 3: How can triangles be used in real-world applications?

Answer: Triangles are used in various applications, including architecture, engineering, and design. For example, triangles are used in the design of bridges, trusses, and roofs due to their inherent strength and stability.

Question 4: What is the significance of the Pythagorean theorem?

Answer: The Pythagorean theorem is a fundamental relation in geometry that states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. This theorem has wide applications in various fields, such as architecture, surveying, and navigation.

Question 5: How are quadrilaterals related to triangles?

Answer: Some quadrilaterals, such as rectangles and squares, can be considered special cases of triangles. For example, a rectangle is a quadrilateral with four right angles, which can be decomposed into two congruent triangles.

Question 6: What is the historical significance of "figuras geometricas planas triangulos y cuadrilateros figuras geometricas planas triangulos y cuadrilateros:"?

Answer: The study of triangles and quadrilaterals has a rich history dating back to ancient times. Mathematicians like Euclid and Pythagoras made significant contributions to the understanding of these shapes and their properties. These concepts have been applied in architecture, engineering, and art throughout history.

In summary, "figuras geometricas planas triangulos y cuadrilateros figuras geometricas planas triangulos y cuadrilateros:" encompasses the study of triangles and quadrilaterals, their properties, relationships, and applications. Understanding these concepts is essential for developing spatial reasoning, problem-solving skills, and appreciating the role of geometry in various fields.

This concludes the frequently asked questions about "figuras geometricas planas triangulos y cuadrilateros figuras geometricas planas triangulos y cuadrilateros:".

Conclusion

In conclusion, "figuras geometricas planas triangulos y cuadrilateros figuras geometricas planas triangulos y cuadrilateros:" encompasses the study of triangles and quadrilaterals, their properties, relationships, and applications. Understanding these concepts is essential for developing spatial reasoning, problem-solving skills, and appreciating the role of geometry in various fields, such as architecture, engineering, and design.

The exploration of triangles and quadrilaterals provides a foundation for understanding more complex geometric shapes and their applications in the real world. By delving into the intricacies of these fundamental shapes, we gain insights into the underlying principles that govern the world around us and develop a deeper appreciation for the beauty and elegance of geometry.

The Ultimate Guide To Minecraft Protection: Safeguarding Your World
Uncover The Core Elements Of Your Website: Essential Element Blocks
Convenient And Hassle-Free: Goodwill Pickup Services Near You